Block-Sparse Tensors
Before discussing how to use QN ITensors in your code, it is helpful to consider examples of block-sparse tensors to define terms and notation.
Consider the Hilbert space of a single "hard-core" boson. This means a system with two states: the vacuum or empty state @@|0\rangle@@ and the occupied state @@|1\rangle@@ with one boson.
Let us define three operators @@a@@ , @@a^\dagger@@ and @@n@@ by their action on the states:
For cases not specified above, the action of each operator gives the result zero. The operator @@a@@ annihilates a boson; @@a^\dagger@@ creates a boson; and @@n@@ measures the boson number.
Arrow Conventions
Diagrammatically, the equation @@a |1\rangle = |0\rangle@@ looks like

Unlike plain, dense ITensors, these tensors have arrows on their indices. There are two kinds of arrows: in and out relative to the tensor. The absolute direction of the arrow on the page (up, down, left, right) will not be important.
We will continue to discuss arrows in more detail, but for now observe that:
- physical (ket) indices have an out arrow
- operators have one incoming index and one outgoing index
- contracted index pairs have opposite arrow directions
In classical tensor notation, an out arrow corresponds to a raised index and an in arrow to a lowered index.
Quantum Numbers
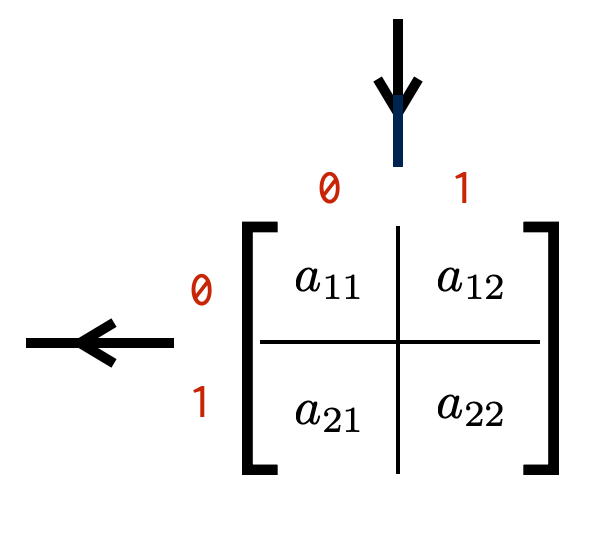
We can write @@a@@ as the following matrix:

The arrows on the row and column indices match the ones in the diagram above. The small red numbers along the outside of the matrix are the quantum numbers labeling the boson number of each index value.
Quantum Number Blocks
The definition of @@a@@ is that it lowers the particle number by one. Therefore if we divide the elements of @@a@@ into quantum number blocks
it follows that the only non-zero block must be the one containing @@a_{1 2}@@ . If any other block were non-zero, there would be cases where acting with @@a@@ would increase the particle number or keep it the same (or some superposition thereof).
Quantum Number Flux
We can go further by considering a generic operator, and labeling each of its blocks by how much they change the boson number.

We will call these numbers the flux of a block. To understand this name, if we associate an out arrow with a plus sign and an in arrow with a minus sign, then we can compute the flux of a block as follows: for each index, multiply the quantum number of the block times the arrow direction of the index; the sum is the flux.
Going in the order row, column, for the upper right block we compute a flux: @@\mbox{}+0 - 1 = -1@@ .
For the lower left block we compute a flux: @@\mbox{}+1 - 0 = +1@@ .
QN ITensors
An QN ITensor is defined as a tensor whose blocks all have the same flux. When we speak of the flux of a QN ITensor, we mean the flux of any of its non-zero blocks. Acting an operator which is a QN ITensor onto a state changes the state's quantum number by the flux of that ITensor.
The operators @@a@@ , @@a^\dagger@@ , and @@n@@ above are all QN ITensors. We can confirm this for @@a^\dagger@@ and @@n@@ by checking that their non-zero elements are only in blocks of the same flux:
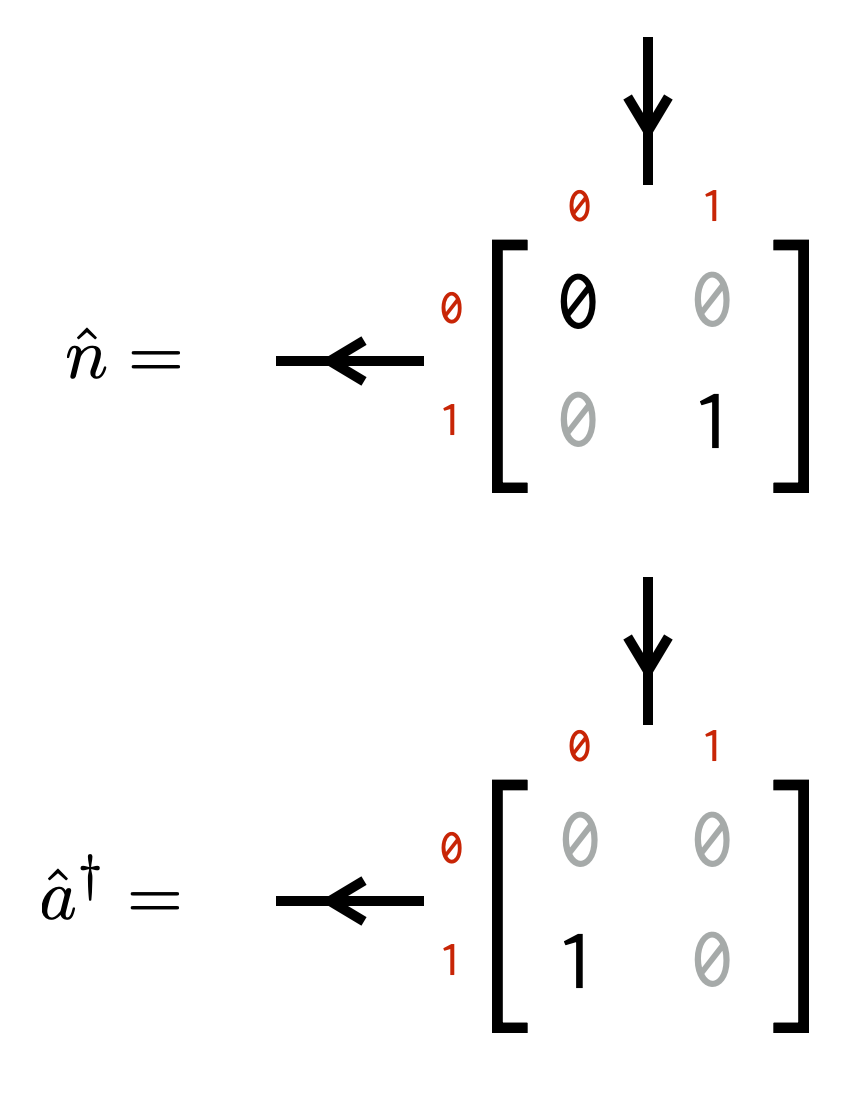
Test your knowledge: what are the fluxes of the @@n@@ and @@a^\dagger@@ operators?
An operator such as @@(n+a^\dagger)@@ would be a valid operator, but would not be a well-defined QN ITensor.