Introduction to Factorizing ITensors
The real power of tensor algorithms comes from tensor factorization, which can achieve huge compression of high-dimensional data. For example, a matrix product state (a.k.a. tensor train) can be viewed as the successive factorization of a very high rank tensor.
The ITensor approach to tensor factorizations emphasizes the structure of the factorization, and does not require knowing the index ordering.
ITensor offers various tensor factorizations, but in this chapter we focus on the example of the SVD, which is used frequently in physics applications.
Singular Value Decomposition
The singular value decomposition (SVD) is a matrix factorization that is also extremely useful for general tensors.
As a brief review, the SVD is a factorization of a matrix M into the product
with U and V having the property @@U^\dagger U = 1@@ and @@V^\dagger V = 1@@ . The matrix S is diagonal and has real, non-negative entries known as the singular values, which are typically ordered from largest to smallest. The SVD is well-defined for any matrix, including rectangular matrices. It also leads to a controlled approximation, where the error due to discarding columns of U and V is small if the corresponding singular values discarded are small. For more background reading on the SVD, see our SVD article.
To compute the SVD of an ITensor, you only need to specify which indices are (collectively) the "row" indices (thinking of the ITensor as a matrix), with the rest assumed to be the "column" indices.
Say we have an ITensor with indices i,j, and k
auto T = ITensor(i,j,k);
and we want to treat i and k as the "row" indices for the purpose of the SVD.
To perform this SVD, we can call the function svd as follows:
auto [U,S,V] = svd(T,{i,k});
The notation auto [U,S,V] is a convenient C++17 feature that captures multiple return
values from a function and defines the variables U, S, and V all in one line.
U, S, and V are ITensors.
Diagrammatically the SVD operation above looks like:
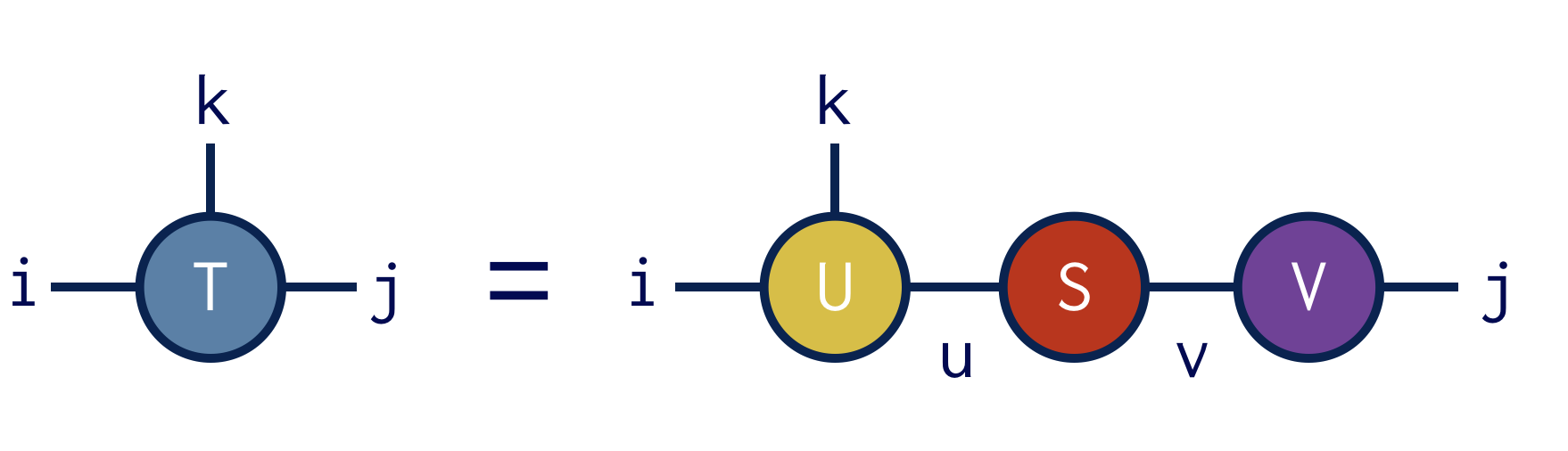
The guarantee of the svd function is that the ITensor
product U*S*V gives us back an ITensor identical to T:
Print(norm(U*S*V - T)); //typical output: norm(U*S*V-T) = 1E-13
#include "itensor/all.h"
#include "itensor/util/print_macro.h"
using namespace itensor;
int main()
{
auto i = Index(3,"i");
auto j = Index(4,"j");
auto k = Index(5,"k");
auto T = randomITensor(i,j,k);
auto [U,S,V] = svd(T,{i,k});
Print(norm(U*S*V-T));
return 0;
}
Truncating the SVD spectrum
An important use of the SVD is approximating a higher-rank tensor by a product of lower-rank tensors whose indices range over only a modest set of values.
To obtain an approximate SVD in ITensor, pass one or more of the following accuracy parameters:
"Cutoff"— real number @@\epsilon@@ . Discard the smallest singular values @@\lambda_n@@ such that the truncation error is less than @@\epsilon@@ :$$ \frac{\sum_{n\in\text{discarded}} \lambda^2_n}{\sum_{n} \lambda^2_n} < \epsilon \:. $$Using a cutoff allows the SVD algorithm to truncate as many states as possible while still ensuring a certain accuracy.
"MaxDim"— integer M. If the number of singular values exceeds M, only the largest M will be retained."MinDim"— integer m. At least m singular values will be retained, even if some fall below the cutoff
Let us revisit the example above, but also provide some of these accuracy parameters
auto T = randomITensor(i,j,k);
auto [U,S,V] = svd(T,{i,k},{"Cutoff=",1E-2,"MaxDim=",50});
In the code above, we specified that a cutoff of @@\epsilon=10^{-2}@@ be used and that at most 50 singular values should be kept. We can check that the resulting factorization is now approximate by computing the squared relative error:
auto truncerr = sqr(norm(U*S*V - T)/norm(T));
Print(truncerr);
//typical output: truncerr = 9.24E-03
Note how the computed error is below the @@\epsilon@@ we requested.
#include "itensor/all.h"
using namespace itensor;
int main()
{
auto i = Index(30,"i");
auto j = Index(40,"j");
auto k = Index(50,"k");
auto T = randomITensor(i,j,k);
auto [U,S,V] = svd(T,{i,k},{"Cutoff=",1E-2,"MaxDim=",500});
auto truncerr = sqr(norm(U*S*V-T)/norm(T));
Print(truncerr);
return 0;
}