Applying a Single-site Operator to an MPS
In many applications one needs to modify a matrix product state (MPS) by multiplying it with an operator that acts only on a single site. This is actually a very straightforward operation and this formula shows you how to do it in ITensor.
Say we have an operator @@G^{s'_3}_{s_3}@@ which
which acts non-trivially on site 3 of our MPS psi
as in the following diagram:
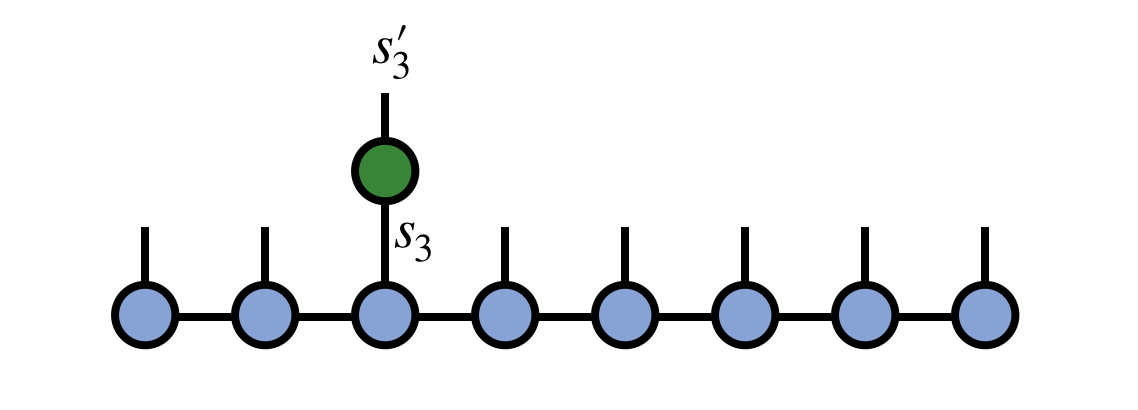
To carry out this operation, contract the operator G with the MPS tensor for site 3, removing the prime from the @@s'_3@@ index afterward:
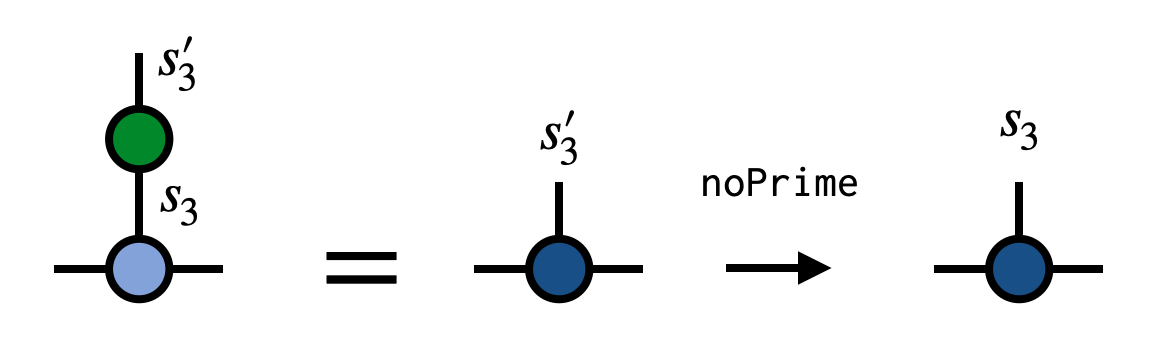
auto newA = G*psi(3);
newA.noPrime();
Finally, put the new tensor back into the MPS to update the third MPS tensor:
psi.set(3,newA);
Or alternatively psi.ref(3) = newA;.
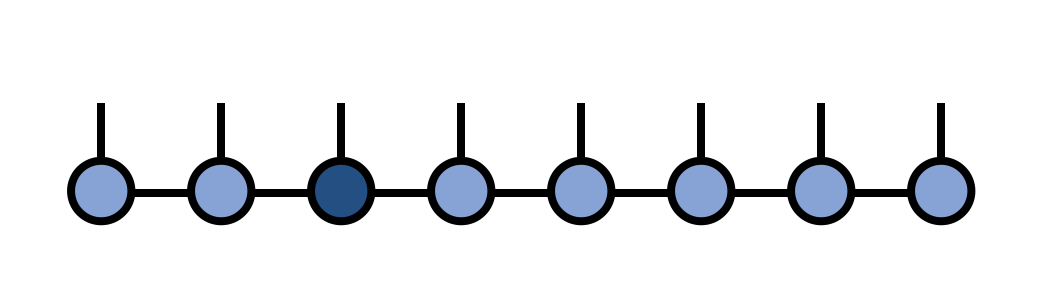
Afterward, we can visualize the modified MPS as:
As a technical note, if you are working in a context where gauge or orthogonality
properties of the MPS are important, such as in time evolution using two-site gates
(see the two-site gate formula), then you may want to call psi.position(3)
before modifying the tensor at site 3, which will ensure that the MPS remains in a
well-defined orthogonal gauge. Modifying a tensor which is left- or right-orthogonal
(i.e. not the "center" tensor of the gauge) will destroy the gauge condition and
require extra operations to restore it. (Calling the .position method will automatically
fix this but will have to do extra work to do so.)