QN Index
We have seen that indices of quantum-number conserving tensors have quantum number subspaces. That is, some values the index takes correspond to a quantum number q1; other values of the index correspond to q2; etc. (These quantum numbers are the small red numbers in the figure below.)
Let us revisit our example from the last chapter of a single-site operator acting on the Hilbert space of a single hard-core boson:
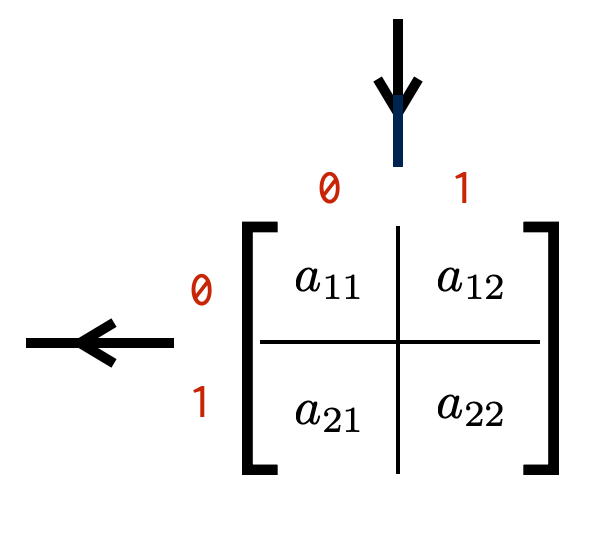
We see that for each index, if the index value is 1 then it is in the quantum number 0 subspace. If the index value is 2, the index is in the quantum number 1 subspace. Below we will see that more generally, multiple index values can fall into the same quantum number subspace.
Constructing a Simple QN Index
Continuing with the above example, let us construct a tensor index with quantum-number subspaces: a QN Index.
auto I = Index(QN(0),1,
QN(1),1,
Out,"I");
An QN Index contains an ordered collection of QN-integer pairs. Each QN labels the quantum number of a subspace of the Index, and the integer defines the dimension or size of that subspace. In mathematical terms, the Index defines a vector space with an internal direct-sum structure.
In the code above, the QN Index has a tag "I". It has two subspaces, both of size 1. The first subspace has quantum number QN(0). The second subspace has a quantum number QN(1). The arrow direction of I is specified as Out.
The size of this QN Index is 2, because it has two subspaces each of size 1.
Constructing a General QN Index
Now lets construct an QN Index whose subspaces correspond to multiple index values. This can be done by making subspaces whose sizes are greater than 1.
auto J = Index(QN(-2),2,
QN(-1),4,
QN( 0),6,
QN(+1),4,
QN(+2),2,
Out,"J");
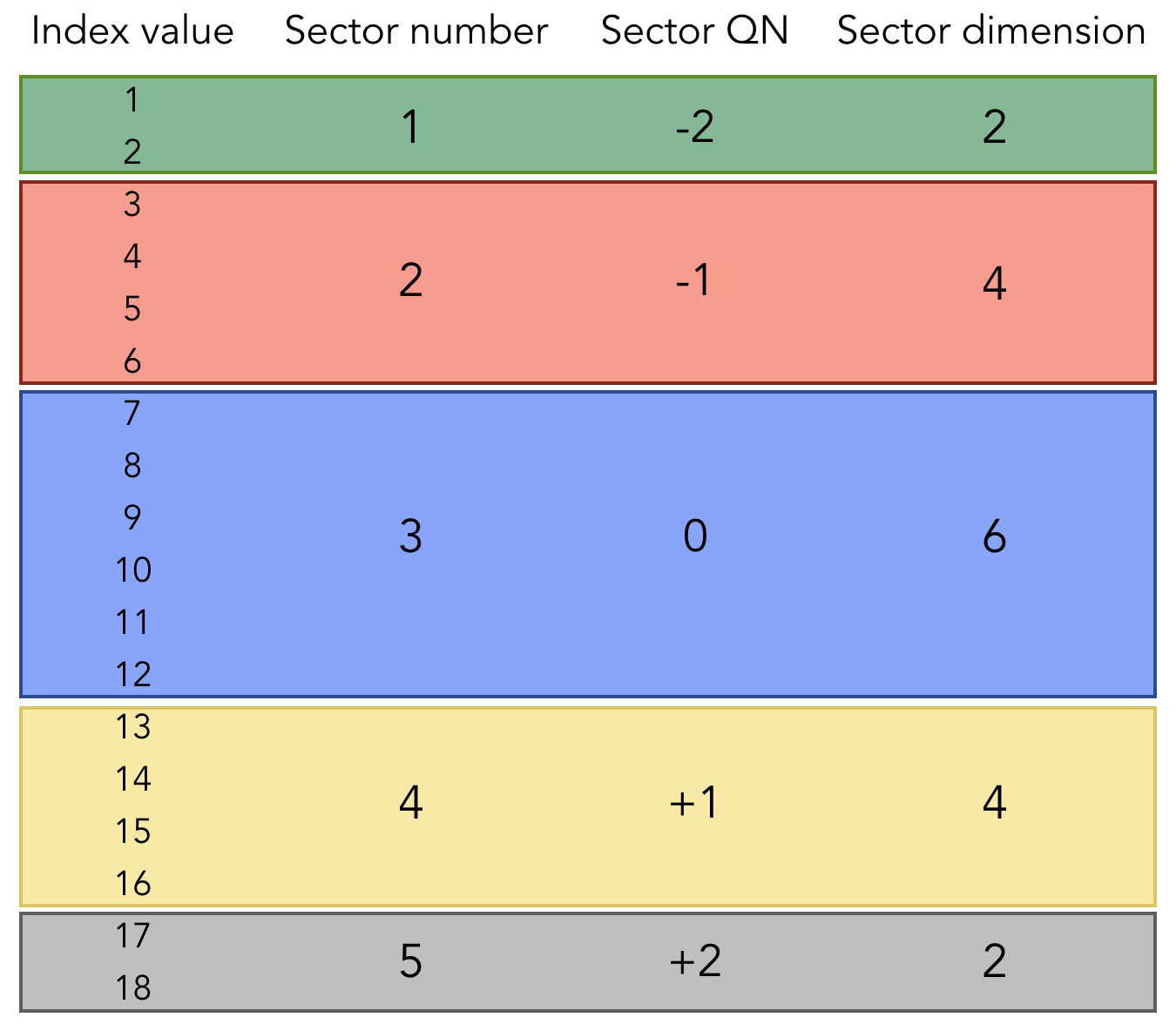
This Index has five subspaces, labeled by five QN-integer pairs.
The first subspace has a size of 3 and an QN (quantum number) of -2.
The second subspace has a size of 5, and a QN of -1.
Overall we can see that the Index J has 5 subspaces of varying sizes and quantum numbers.
The values that J can take (the index values of J) range from 1 up to 18 (=2+4+6+4+2). Values 1 and 2 correspond to the first subspace; values 3 through 6 to the second subspace; etc.
The above example can be summarized in a chart:
Relationship to regular Index objects
A QN Index is of type Index just like a regular Index used for dense ITensors.
But internally, it carries extra information about its subspaces (direct-sum subspaces).
To check whether an Index I carries QN information, you can call hasQNs(I).