// About me
I am a research scientist at the
Flatiron Institute
Center for Computational Quantum Physics (CCQ) where I develop
and apply tensor network computational methods, primarily for quantum many-body systems.
[See my notes on matrix product states and DMRG.]
Tensor networks are a technique to represent very high-order tensors by a contracted network of low-order tensors, allowing one to make an exponential reduction in the parameters needed, while still maintaining accuracy. The prototypical application is the approximation of a many-body quantum wavefunction, but tensor networks are also useful for approximating transfer matrices of classical systems and weights of models used in machine learning.
Download my CV// Experience
Research Scientist — Flatiron Institute
Sep 2017-Present
- Development of the ITensor library, including a port to the Julia language.
- DMRG approach to optimizing PEPS
- Extensions and applications of finite-temperature tensor network methods
Research Scientist — UC Irvine
Feb 2016-Aug 2017- Scalable "sliced basis" approach for applying DMRG to quantum chemistry
- Proposed a machine learning framework based on powerful tensor network techniques developed in physics. Video and talk slides.
Postdoctoral Researcher — Perimeter Institute for Theoretical Physics
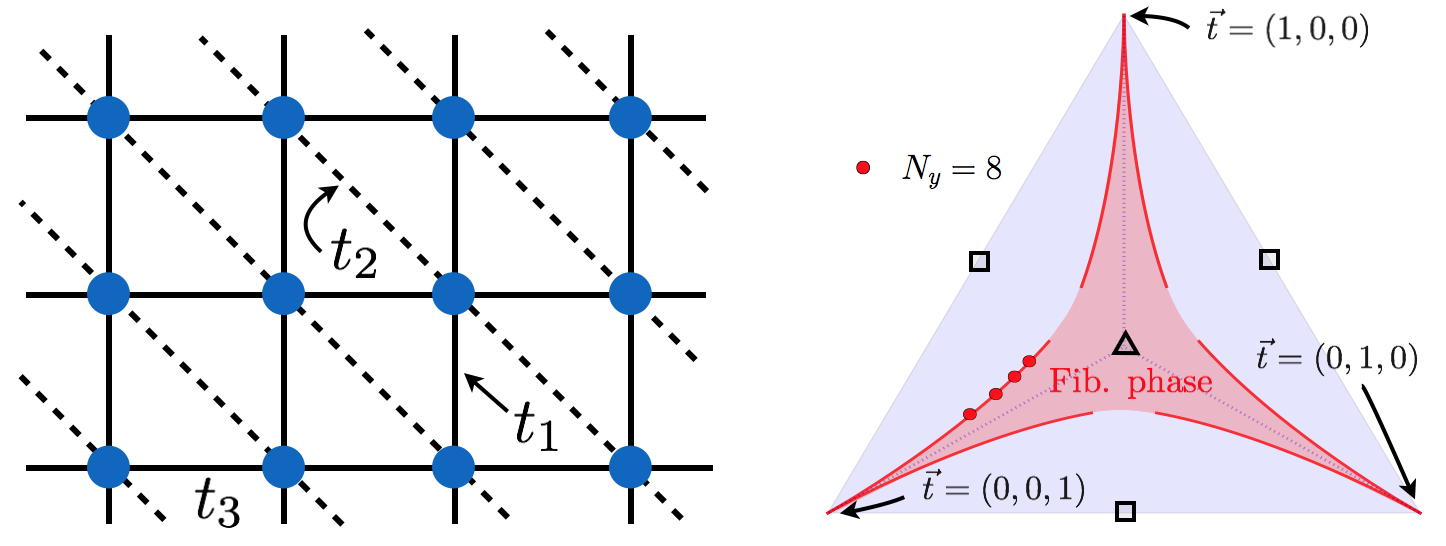
2013-Jan 2016- Showed an isotropic, nearest-neighbor 2d parafermion lattice model hosts a non-trivial phase supporting Fibonacci anyons
- Performed highly cited calculations of universal entanglement terms in critical systems arising from sharp corners
- Significantly expanded the user base of the ITensor library and developed an ambitious new version 2.0 design
Postdoctoral Researcher — UC Irvine
Groups of Steven R. White and Kieron Burke
2010-2013- Discovered a method for parallelizing the density matrix renormalization group in real space.
- Co-developed an open source library for tensor product wavefunction algorithms. Website: http://itensor.org/.
Graduate Student Researcher — UC Santa Barbara
Advisor: Leon Balents
2005-2010- Applied a variety of analytical methods (bosonization, mean-field, spin wave, high temperature series, Monte Carlo) to study frustrated magnets.
- Collaborated with Steven R. White on a new method for simulating finite temperature quantum systems (the METTS algorithm).
// Education
2005-2010 Ph.D. in Physics, UC Santa Barbara. Advisor: Leon Balents 2000-2005 BS in Physics, Georgia Institute of Technology. Highest honors. 2000-2005 BS in Mathematics, Georgia Institute of Technology. Highest honors.// Publications
2020Tai-Danae Bradley, E.M. Stoudenmire, John Terilla, arxiv:1910.07425
Katharine Hyatt, E.M. Stoudenmire, arxiv:1908.08833
Steven R. White, E.M. Stoudenmire Phys. Rev. B, 99: 081110(R) [arxiv:1803.11537]
William Huggins, Piyush Patel, K. Birgitta Whaley, E.M. Stoudenmire Quantum Science and Technology, 4: 024001 [arxiv:1803.11537]
E.M. Stoudenmire, Quantum Science and Technology, 3: 034003 1801.00315 Quant. Sci. Tech., 3: 034003
William Huggins, C. Daniel Freeman, E.M. Stoudenmire, Norm M. Tubman, K. Birgitta Whaley 1710.03757
Benedikt Bruognolo, Zhenyue Zhu, Steven R. White, E.M. Stoudenmire 1705.05578
Mario Motta, David M. Ceperley, Garnet Kin-Lic Chan, John A. Gomez, Emanuel Gull, Sheng Guo, Carlos Jimenez-Hoyos, Tran Nguyen Lan, Jia Li, Fengjie Ma, Andrew J. Millis, Nikolay V. Prokof'ev, Ushnish Ray, Gustavo E. Scuseria, Sandro Sorella, Edwin M. Stoudenmire, Qiming Sun, Igor S. Tupitsyn, Steven R. White, Dominika Zgid, Shiwei Zhang 1705.01608
E.M. Stoudenmire and Steven R. White Phys. Rev. Lett., 119: 046401
E.M. Stoudenmire and David J. Schwab Advances in Neural Information Processing Systems, 29 4799
Sharmistha Sahoo, E.M. Stoudenmire, Jean-Marie Stephan, Trithep Devakul, Rajiv R.P. Singh, and Roger Melko, Phys. Rev. B, 93: 085120
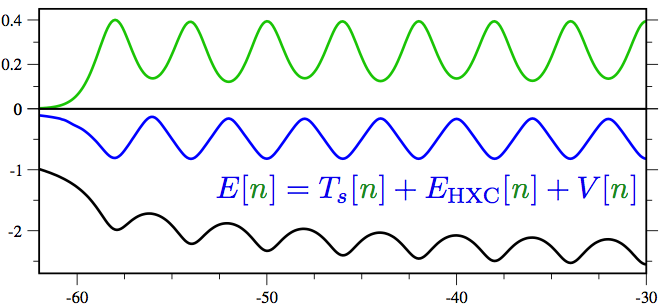
Thomas E. Baker, E.M. Stoudenmire, Lucas O. Wagner, Kieron Burke, and Steven R. White, Phys. Rev. B, 91: 235141
Z. Papic, E.M. Stoudenmire, and Dmitry A. Abanin, Ann. Phys. 362 714
E.M. Stoudenmire, David J. Clarke, Roger S. K. Mong, and Jason Alicea, Phys. Rev. B, 91: 235112 [Editor's suggestion]
E.M. Stoudenmire, Peter Gustainis, Ravi Johal, Stefan Wessel, and Roger G. Melko, Phys. Rev. B, 90: 235106
Lucas O. Wagner, Thomas E. Baker, E.M. Stoudenmire, Kieron Burke, and Steven R. White, Phys. Rev. B, 90: 045109 [Editor's suggestion]
Ann Kallin, E.M. Stoudenmire, Paul Fendley, Rajiv R.P. Singh, Roger G. Melko, J. Stat. Mech. P06009
Lucas O. Wagner, E.M. Stoudenmire, Kieron Burke, and Steven R. White, Phys. Rev. Lett. 111: 093003 [Editor's suggestion]
E.M. Stoudenmire and Steven R. White, Phys. Rev. B 87: 115137
Salvatore R. Manmana, E.M. Stoudenmire, Kaden R.A. Hazzard, Ana Maria Rey and Alexey Gorshkov, Phys. Rev. B 87: 081106(R)
E.M. Stoudenmire, Lucas O. Wagner, Steven R. White and Kieron Burke,
Phys. Rev. Lett. 109: 056402
Lucas O. Wagner, E.M. Stoudenmire, Steven R. White and Kieron Burke,
Phys. Chem. Chem. Phys. 14: 8581
E.M. Stoudenmire and Steven R. White, Annual Reviews of Condensed Matter Physics 3: 111
E.M. Stoudenmire, Jason Alicea, Oleg A. Starykh and Matthew P.A. Fisher, Phys. Rev. B 84: 014503 [Editor's suggestion, Synopsis Article]
E.M. Stoudenmire and Steven R. White, New J. Phys. 12: 055026
E.M. Stoudenmire, Simon Trebst and Leon Balents, Phys. Rev. B 79: 214436
E.M. Stoudenmire and Leon Balents, Phys. Rev. B 77: 174414
E.M. Stoudenmire and C.A.R. Sá de Melo, J. Appl. Phys. 97: 10J108