Low number of states for large chains means metastable states? Is it possible work with arbitrary precision in Itensor?

Question

Hi!

I'm trying to explore the ionic hubbard model in 1d, but I have some problems for large chains. For some set of parameters I could compute ground state energy, charge and spin gap energies with enough accuracy for large chain (up to 300 sites) but there is some regions of parameters where a metastable state seems to appear because the algorithm does not need a large number of states to converge, high noise and number of the states even does not solve my problem (even I have this problem in other code without tensor network in Fortran 98)

I'm thinking that, for large chains and some parameters, the numerical error of elementary operations can be of the same order that the fluctuations of the dmrg iterations such that the current precision in the double floating point is actually low. Is there some how I can work with an arbitrary precision? Or Someone have an idea of how I can explore large chains?

Comments

Hi, thanks for the question but it's a little bit hard to answer. Are you just saying that you believe the algorithm is getting stuck into a metastable state or local minimum which is not the ground state? That can happen with DMRG sometimes, and usually choosing a good initial state is the solution. But it can be hard to pick a really good one sometimes.

What I'm having a harder time understanding is the part of your question about needing higher precision. If your state is not very close to the ground state, then resolving the energy to many digits of precision won't be of a lot of value since you would be resolving an incorrect energy very precisely. So I think what you are saying instead is that the reason DMRG may be getting stuck is because of an accumulation of floating point roundoff error? Personally I have not heard of or encountered this phenomenon in a DMRG calculation before but I'm happy to discuss if you have identified a specific scenario where you think this is the culprit.

Finally one last question is why you need to go to such long systems. On the one hand it's usually very possible to go to many hundreds or even thousands of sites with DMRG, so it can be a nice thing to do when it works and when it helps with a particular problem. But as you probably know, for many problems system sizes of a few hundred at most are often plenty large enough to resolve any finite-size effects. Does your system happen to have particularly severe finite-size effects or particularly large length scales in some way?

Best,
Miles

Answer 1

Hi, Miles!

Thanks for answer so soon and sorry for said a lot of strange things, may be I can explain better what I have seen in my simulation.

I'm trying to reproduce all results of the following paper of S. R. Manmana et. al "https://journals.aps.org/prb/abstract/10.1103/PhysRevB.70.155115" about the Ionic Hubbard Model. In particular, I want to calculate the finite-size scaling behavior of spin gap for this model.

I have perfomed several calculations in the region with delta=20.0 and U=21.0 to U=22.0 for a lattice length from L=64 up to L=512. In all most values of this parameter region I have a good finite-size scaling of the gap as it is reported by Manmana, but fot values near to U=21.0 or less than this value, the spin gap suddenly jump for lattices with L>128. This is a figure of this behaviour.

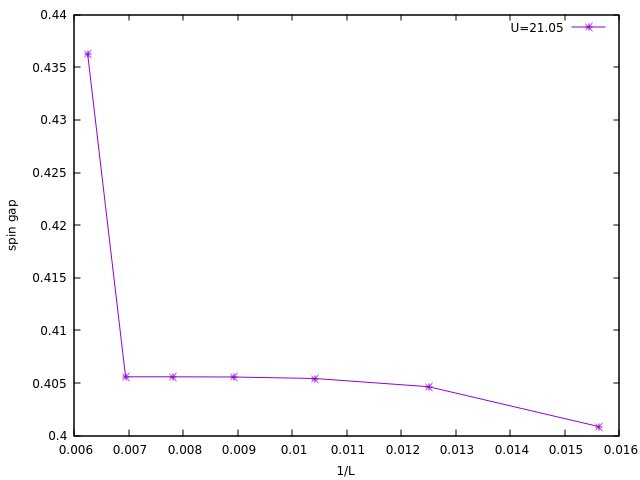
I did check the information of DMRG steps by locking for some problem and I found out that the number of states were very small (from 64 to 100 states) with respect to the same calculation for a higher value of U (U=21.45 where at least 400 states are required for the same lattice length). Due to this problem I increase the number of states at least to 800 states, the maximum value considerer by Manmana, but I obtained the same result of the energy.

I'm trying to understand what is happening in this system and the only thing that could explain this behaviour is may be an accumulation of floating point roundoff error as you well interpreted from my first question. The strangest thing is that I have observed this behavior not only using tensor networks, but also in other Fortran code without mps.

This are the DMRG parameters for this simulations

    maxdim  mindim  cutoff  niter  noise
   100        1     1E-5     6      1E-5
   200        1     1E-6     6      1E-5
   256        1     1E-7     6      1E-8
   400        1     1E-8     5      1E-9
   400        1     1E-8     5      1E-10
   800        1     1E-9     5      1E-11
   800        1     1E-9     4      1E-11
   800        1     1E-9     4      1E-12