Hi all
I'm was hoping to calculate the entanglement entropy for 2D Kitaev's honeycomb lattice. I followed one of Miles' advice posted in 2017:
Re-do the DMRG calculation with the 1D ordering of the sites changed so that your MPS first visits every site in your cluster (in a 1D MPS path sense) before visiting the rest of the sites outside of your cluster. Then just compute the entanglement in the usual 1D fashion across the MPS bond separating the cluster from the rest.
Yet I came across a problem where the ground state energy changes if I re-order the lattice. In the lattice labeled below I got the correct gs energy as compared with ED result: E0 = -3.57 with PBC.
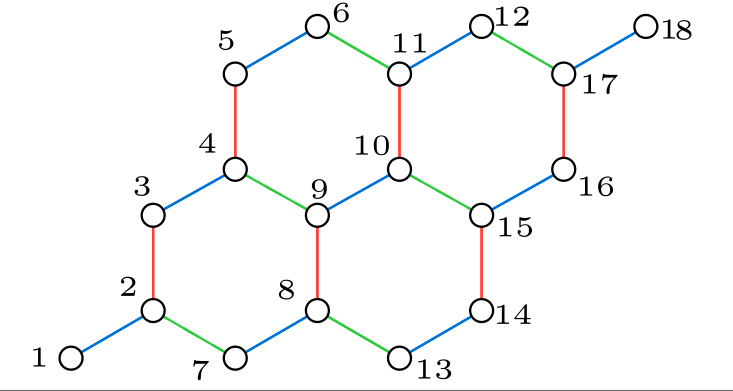
Now I'd like to calculate entanglement entropy of the lower left plaquette, so I re-ordered the label in the following:
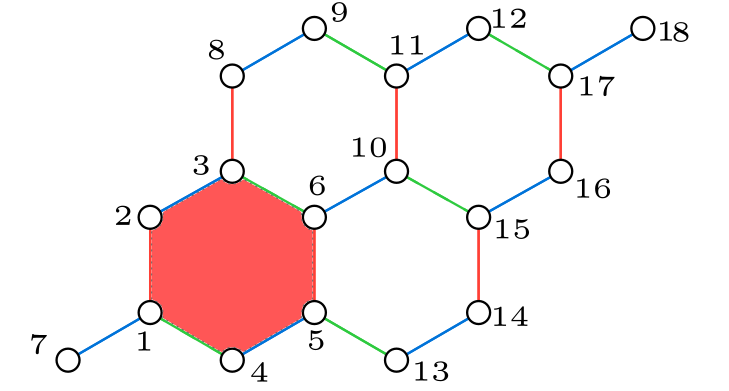
such that the red plaquette (1,2,3,4,5,6) is constructed first by Itensor, and I can make a 1D cut thereafter to keep only those in red. The relevant code is:
auto lattice = honeycombLattice(Nx,Ny,{"YPeriodic=",yperiodic,"XPeriodic=",xperiodic});
auto ampo = AutoMPO(sites);
// Isotropic Kitaev interaction
for(auto bnd : lattice)
ampo += bnd.type, bnd.s1, bnd.type, bnd.s2;
where honeycombLattice is a function defined by myself, all bonds can be printed:
(2,1,Sz)
(6,5,Sz)
(8,3,Sz)
(9,7,Sz)
(11,10,Sz)
(12,4,Sz)
(15,14,Sz)
(17,16,Sz)
(18,13,Sz)
(4,1,Sy)
(6,3,Sy)
(11,9,Sy)
(13,5,Sy)
(14,7,Sy)
(15,10,Sy)
(16,2,Sy)
(17,12,Sy)
(18,8,Sy)
(3,2,Sx)
(5,4,Sx)
(7,1,Sx)
(9,8,Sx)
(10,6,Sx)
(12,11,Sx)
(14,13,Sx)
(16,15,Sx)
(18,17,Sx)
which looks without error. But Here I got ground state energy E_0 = -3.518 which is different from that of the former ordering. So I'm wondering if I missed something important here. Or also possibly some nuance in the code.
Any advice will be helpful, Thanks!